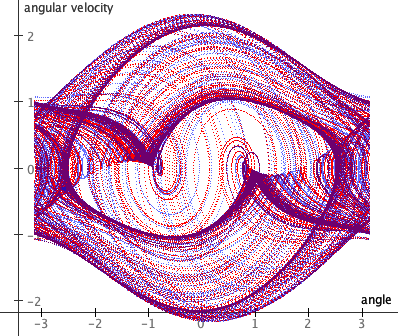
graph of angular velocity vs. angle for two chaotic pendulums
Physics-based simulation of two driven pendulums that start almost identically; this demonstrates sensitivity to initial conditions of chaotic systems. It looks like a single pendulum at first, but wait for a minute and you will see the two pendulums diverge in their behavior.
Click the "Sim" tab to access parameters such as: starting angle difference, drive amplitude, frequency, mass, gravity, and damping. You can drag the pendulum with your mouse to change the starting position.
The pendulums are continuously driven by an external torque force that varies between twisting clockwise and counterclockwise. This torque force is represented by the curved arrow, the length of the arrow corresponds to the strength of the force.

These are two independent pendulum simulations running simultaneously. They start with almost identical initial conditions, but just slightly different starting angles (the difference is the angle difference parameter). Running for several minutes produces the graph shown at left.
You will notice that the pendulums stay in sync for a while, then drift slightly apart, and then are soon completely different in their behavior. This is an example of sensitivity to initial conditions which is a hallmark of chaotic systems. This is also known as the Butterfly Effect whereby a butterfly flapping its wings in North America could cause a storm to occur in South America.
The angle difference parameter specifies the difference between the start angle of the two pendulums. Try different values for the starting angle difference, and measure how much time it takes for the pendulums to diverge significantly. If you make a graph of this (difference in starting angle vs time to divergence), is it a linear or exponential curve? Is this different to how a linear system would respond?
For the math behind the simulation see the page about the Chaotic Driven Pendulum; this is the same simulation as that one, except here there are two pendulums.
Also available: source code, documentation and how to customize.