
There are unusual chemical reactions that exhibit oscillating behavior that can persist for a long time. Below are links to videos of simulations of such a reaction-diffusion system. The simulations were done using Matlab, see the paper for details.
We have a two-dimensional space (eg. a thin fluid) with two chemical species U, V which react with each other, and also diffuse (spread out) on their own. The system is defined by the equations
Ut = λ(A)U − ω(A)V + D ∇2U
Vt = ω(A)U − λ(A)V + D ∇2V
where A 2 = U 2+V 2 and ∇2 = ∂x2 + ∂y2 . The diffusion constant is D . The λ and ω functions are defined by
λ(A) = ε − a A2
ω(A) = c − β A2
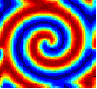
The movies show the concentration of only one of the two chemical species, U . The concentration is represented by colors, with blue being low concentration, through light-blue, green, yellow to red which is the highest concentration. The first four movies show various initial conditions. The parameters used are: ε = 1, a = 1, c = 0, β = 1, D = 0.1 .
The next several movies show the effect of modifying the parameters in the defining equations of the system. The parameters used are: ε = 1, a = 1, c = 0, β = 1, D = 0.1 unless otherwise noted. The initial condition is the one-armed spiral in each movie.
This web page was first published February 2002.